The thing on my mind today is what has been dubbed the ‘official mathematical equation’ for finding the number of polyamorous relationships among a group of people. For the past three years, I've been convinced that this is wrong, and I'm finally putting my proof (I hope) online.
This isn't a light bulb joke. But it could be, if you wanted it to. In a weird way involving advanced discrete mathematics and polyamorous math geeks.
The thing on my mind today is what has been dubbed the ‘official mathematical equation’ for finding the number of polyamorous relationships among a group of people. For the past three years, I've been convinced that this is wrong, and I'm finally putting my proof (I hope) online.
It grates on me that I see the formula on t-shirts and merchandise because I'm such an obsessive, anally retentive perfectionist. And this is my own soap box.
The What Now?
It wasn't a stormy night. It was a cold winter evening in 2006. I was made aware of this interesting Livejournal post (and this amendment). The post claimed an equation ‘that will tell you for any size group of people n how many possible relationship configurations (couples, triads, and so on) are possible within that group’.
The final, amended equation looks like this:
‘Fun’, I thought to myself when I saw this, and ‘this should grow incredibly quickly’. Let's find out. I took out my trusty calculator (it was a small Ruby program, actually) and worked out a few values.
| People (n) | Result |
|---|---|
| 2 | 1 |
| 3 | 4 |
| 4 | 11 |
| 5 | 26 |
| 6 | 57 |
| 7 | 120 |
| 8 | 247 |
| 9 | 502 |
| 10 | 1013 |
This doesn't seem to grow as rapidly as you'd expect. So I set out trying to prove whether or not the formula is wrong.
Impatient? Here It Is
The formula simplifies to a simple, but rather mundane:
However, simplified or not, it's still wrong.
Detailed results (including several similar problems and their answers) are available here as a PDF document, and also as the Polyamory Graph Explorer widget (which allows you to play what-if with polyamorous relationship graphs).
Feel free to read on for more details!
Wait a Minute. ...‘Poly’?
Sort for polyamorous, a nasty neologism if ever there was one1. It denotes the tendency, ability, or desire to be involved romantically with more than one person at a time, with the consent of all people involved.
This raises lots of philosophical questions, arguments, and wailing and gnashing of teeth. Usually the word Right is mentioned, and the capital R is pronounced very clearly.
But this isn't about the viability of the polyamorous lifestyle. Come to your own conclusions (hint: it can and does work for some, but for everyone — just like monogamy, funnily enough).
This is about the graph theory lurking behind polyamorous relationships. You see, when Alice and Bob establish a relationship, things are incredibly simple. Alice and Bob are together. The standard juvenile question ‘Who's your boy-/girlfriend?’ is simple to answer.
When Alice has a relationship with Sam, however, and she gets together with Bob, things become complicated. Even more so if Sam also has a relationship with Phil and John (who's interested in Alice). Poly people tend to sit down and draw diagrams of their relationships to explain how they're attached to others. Eventually, fairly advanced graph theory concepts are easy to grasp, and the ‘how many ways’ question can and will pop up.
Incidentally, if you need some more information about polyamory, I suggest Polyamory.org. Also, Franklin ‘Tacit’ Veaux's home page is an excellent source of information on polyamory.
What Do You Mean, ‘Inelegant’?
Any self-confessed mathematics geek knows the meaning of mathematical elegance. It's an elusive concept, this one, but it involves perfection via simplicity. You don't express \(2 + 2\) as \(2 + 4 - ⌊√5⌋\), even though both expressions produce the same result. You generally don't leave your expressions unsimplified (remember that maths teacher at school who used to take marks off because you hadn't quite reached the absolutely final, simplest result? That's why).
That doesn't necessarily make the formula wrong, just inelegant2. Let's simplify it and see (if you've studied discrete mathematics, you've probably already noticed what this is). Here's the formula again, for reference:
The aforementioned discrete maths geeks will have noticed the summed bit is the ‘n-choose-k’ formula from combinatorics: it counts the number of ways in which k people can be chosen from a group of n people. This is also known as the binomial coefficient \({n}\choose{k}\) because of its use in algebra. Let's start rewriting:
It's already much simpler! Now, let's examine the summation. We're summing from 2 to n-1, then adding 1. But note that:
This means that we can incorporate that lone +1 into the summation, by summing from 2 to n, and not adding 1:
But wait! We're not done. Remember Pascal's Triangle? If so, recall that \(n\choose k\) is the \(k+1\)-th item on the \(n\)-th row of the triangle. Then, recall that each row of the triangle sums up to \(2^n\):3
Armed with this piece of mathematical esoterica, we can simplify more:
What Do You Mean, ‘Wrong’?
The formula is wrong (in this context) because it doesn't answer a specific enough question, and even once all the combinations of assumptions are attempted, it still doesn't answer any of them.
The Question
The major stumbling block in this is that the problem itself isn't described well enough. It says the formula is supposed to give you the number of ‘relationship configurations’ within a group of people without actually telling us what a ‘relationship configuration’ is.4
Does a relationship configuration include the case where everyone in the group is single (no relationships)? The formula seems not to intend to do this, but it's not certain.
Does a relationship configuration include couples? It seems to, based on an explanation.
Does a relationship configuration allow for single people in the group?
Does a relationship configuration involve one and only one set of directly or indirectly connected people, or can any number of different polyamorous subgroups exist in the group?
Are we talking about specific people, or topologies? People are simpler to calculate with, but the results are several orders of magnitude higher than those this formula comes up with. Topologies are horrendously difficult to enumerate, and need some seriously advanced maths, which may explain why this formula is wrong.
The Answer
Let's assume that the question was completely off, and construct a fake one. How many fully-connected sub-graphs can we find in a labelled, undirected n-graph?
In polyamorous terms, what is the total number of potential couples, triads, quads, quints, et cetera, in an n person group? For polyamory newbies, a couple is a relationship between two people; a triad is a three person poly group where each person is in a relationship with every other person; a quad is like a triad, but with four people in six relationships (everyone with everyone); and so on.5
Now we're in business. We no longer need advanced graph theory, all we need is basic high school combinatorics.
There is a single two-person sub-group in a two person group (duh). In a three-person group, there are three (AB, AC, BC). In fact, the number of k person subgroups in an n-person group is \(n\choose k\). Aha!
So, if we want to find the number of 2, 3, …, n-person fully-connected sub-groups, all we need to do is:
Ah, very familiar! And it seems like it would work, but for two problems.
Won't Account for All Relationships
Not everyone in a polyamorous group of people is romantically attached to everyone else. Say Alice is in a relationship with Bob and Bill, who are both heterosexual males. Any polyamorous person would recognise this as a polyamorous relationship, the topology of which is called a ‘vee’ (guess why). This equation can't account for it unless Bob and Bill are also in a relationship.
In fact, here are all eight ways three people may be related or unrelated:

The poly equation says there are four polyamorous relationships here: the three couplings (each with one single person in the group), and the last case, where everyone is attached to everyone (the triad). The three vees are completely unaccounted for.
Won't Account for Multiple Sub-Groups
Consider this five-person group:

There are three people in a triad, and two people in a coupling. Both of these relationships are tallied by the equation on their own, but not when they both appear at the same time.
In fact, for any group of over three people, we can have multiple, independent relationships. There can be two independent couples in a four person group; a group of six people can have a quad and a coupling or two triads or three couplings; and so on. The original formula fails to account for this.
Making It Right
To make the formula count actual polyamorous relationships, we need to decide on what we consider a poly relationship in a group of n people. I chose not to make this decision for you — instead, I produced seven problems and worked out some of their surprising formulae (also surpsiringly difficult to formulate).
The main questions are whether or not single people should be allowed in the graph, and whether or everyone should somehow be connected, or disconnected subgraphs are allowed (e.g. five people, in which three are in a triad, and two in a mono relationship).
Labelled Graphs
Problem 1. What is the number of ways a group of n specific people may be pairwise related or unrelated such that there are zero or more relationships within the group?
Problem 2. What is the number of ways a group of n specific people may be pairwise related or unrelated such that there are one or more relationships within the group? The answer to this is trivial: it's the answer to Problem 1 minus one. There's exactly one n-person graph in which any number of people may be completely unrelated, after all.
Problem 3. What is the number of ways a group of n specific people may be pairwise related or unrelated such that there is at least one relationship within the group, and no single people?
From a graph theory standpoint, this problem calls for the counting of undirected, labelled graphs of at least one edge, and no isolated vertices.
Problem 4. What is the number of ways a group of n specific people may be pairwise related or unrelated in such a way that every person is related, directly or indirectly, to every other person?
In graph theory terms, what is the number of undirected, labelled, connected n-graphs?
Unlabelled Graphs
These much harder problems are about unlabelled graphs, and examine abstract ‘relationship configurations’, not relationships between specific people.
Problem 5. How many of the graphs enumerated in Problem 1 are not isomorphic? That is, how many different shapes are there for n-person graphs? For three people, there are eight different graphs listed by Problem 1, but only four of these are different shapes: the empty graph (no relationships), two people in a relationship and a single, a vee, and a triad.
Problem 6. How many of the graphs counted by Problem 5 have at least one relationship? An easy problem: all but one. For three people, there are three such graphs.
Problem 7. How many of the graphs from Problem 5 are connected? There may be no singles, and no isolated polyamorous groups in the graph. There is an answer to this problem, but is quite difficult to arrive at without advanced discrete maths.
You can read all about it here:
The Polyamory Graph Explorer Widget
You can also play with the Polyamory Graph Explorer, an interactive tool to help you visualise polyamorous relationships.
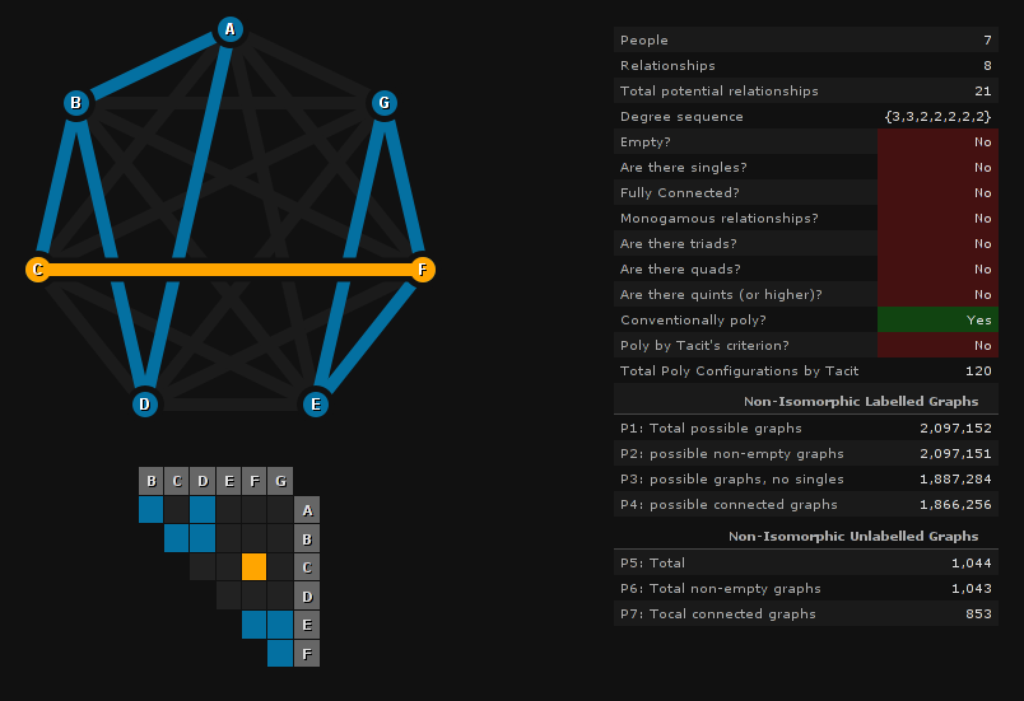
A screenshot of the Polyamory Graph Explorer widget at work.